Nội dung

Gia sư biên hòa nói về đường tiệm cận của hàm số

Gia sư Biên Hòa Đồng Nai nói về đường tiệm cận của hàm số, cung lồi, cung lõm và điểm uốn

1. Khái niệm về cung lồi, cung lõm và điểm uốn

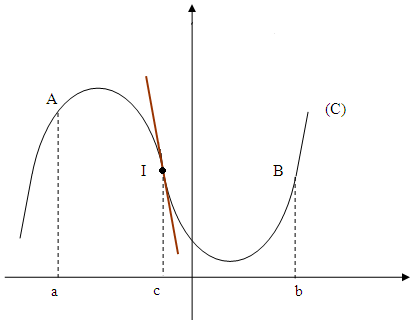
Xét đồ thị hàm số y = f(x), giả sử đồ thị hàm số có tiếp tuyến tại mọi điểm với đồ thị ABC có dạng hàm bậc ba có 2 cực trị. Tại mọi điểm của cung AC, tiếp tuyến luôn ở phía trên của cung AC. Ta nói, cung AC là một cung lồi. Nếu a là hoành độ của điểm A, c là hoành độ của điểm C, thì khoảng (a ; c) được gọi là một khoảng lồi của đồ thị. Tại mọi điểm của cung BC, tiếp tuyến luôn luôn ở phía dưới của cung BC. Ta nói cung BC là một cung lõm. Kí hiệu b là hoành độ của điểm B thì khoảng (c ; b) được gọi là khoảng lõm của đồ thị. Điểm phân cách cung lồi và cung lõm được gọi là điểm uốn của đồ thị.

CHÚ Ý

- Tại điểm uốn tiếp tuyến đi xuyên qua đồ thị.

- Trong một số giáo trình, nhất là giáo trình Giải tích toán học ở Đại học, người ta gọi cung AC là cung lõm, cung BC là cung lồi.

2. Dấu hiệu lồi, lõm và điểm uốn

Trung tâm gia sư Biên Hòa Đồng Nai có các định nghĩa như sau.

ĐỊNH LÝ 1

Cho hàm số y = f(x) có đạo hàm cấp hai trên khoảng (a ; b).

Nếu f”(x) < 0 với mọi x thuộc khoảng (a ; b) thì đồ thị hàm số lồi trên khoảng đó.

Nếu f”(x) > 0 với mọi x thuộc khoảng (a ; b) thì đồ thị hàm số lõm trên khoảng đó.

ĐỊNH LÝ 2

Cho hàm số y = f(x) có đạo hàm cấp hai trên khoảng (a ; b) và x0 thuộc khoảng (a ; b). Nếu f” (x) đổi dấu khi x đi qua x0 thì điểm M0 (x0 ; f(x0)) là điểm uốn của đồ thị hàm số đã cho.

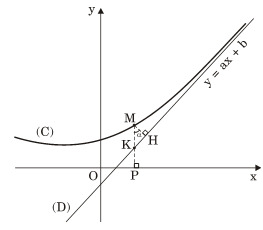
3. Đường tiệm cận

a) Đường tiệm cận ngang

Cho hàm số y = f(x) xác định trên một khoảng vô hạn ( là khoảng dạng a đến dương vô cùng, âm vô cùng đến b hoặc âm vô cùng đến dương vô cùng). Đường thẳng y = y0 là đường tiệm cận ngang ( hay tiệm cận ngang ) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn là giới hạn của hàm số f(x) khi x dần dần tới âm vô cùng hoặc dương vô cùng là y0.

b) Đường tiệm cận đứng

Đường thẳng x = x0 được gọi là đường tiệm cận đứng ( hay tiệm cận đứng ) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau thỏa mãn : giới hạn hàm số f(x) khi x dần tới x0+ là dương vô cùng hoặc âm vô cùng, khi x dần tới x0- là âm vô cùng hoặc dương vô cùng.

Tôi là Trần Lai hiện đang là Co-Founder của Gia Sư Minh Trí. Trong blog của mình tôi chia sẻ các phương pháp học tập hiệu quả, các bài văn hay, thông tin về tác giả, tác phẩm để quý thầy cô, quý phụ huynh và các em học sinh tham khảo. Hi vọng sẽ giúp ích cho quý độc giả

Trần Lai

Các bài viết khác...