Phương trình mũ và cách giải một số bài toán phương trình mũ

Phương trình mũ và cách giải một số bài toán phương trình mũ

Như tiết trước các bạn đã nắm được khái niệm cơ bản về định nghĩa, đạo hàm cũng như khảo sát một hàm số mũ bất kì. Hôm nay, gia sư Biên Hòa sẽ đi sâu vào phương trình hàm số mũ và cách giải phương trình hàm mũ cho các bạn. Trước khi đi vào chi tiết, tôi sẽ nêu một bài toán thực tế áp dụng hàm số mũ. Có một nhà kinh doanh tài giỏi, ông ta có một số tiền lớn và quyết định gửi tiết kiệm với lãi suất khá cao là 9% trên một năm. Lãi hằng năm sẽ được cộng dồn vào vốn, từ đó lãi sẽ ngày càng sinh ra lãi. Vậy hỏi sau bao nhiêu năm nữa thì người đó có số tiền trong tài khoản tiết kiệm gấp đôi số tiền bỏ vô ban đẩu ?

Câu hỏi khá thú vị đúng không ? Đừng nghĩ nó quá khó đối với bạn vì bạn không thuộc lĩnh vực chuyên môn này. Bạn có thể hoàn toàn tìm ra câu trả lời chính xác sau khi học xong bài hôm nay đấy.

Để mở đầu cho phần học, tôi sẽ giới thiệu khái quát về phương trình mũ như sau :

Phương trình mũ cơ bản có dạng a^x = b ( a > 0, a ≠ 1)

Để giải được phương trình trên, ta áp dụng định nghĩa logarit

-         Với mọi số b > 0, ta có a^x = b tương đương với x = \({\log _a}b\).

-         Với mọi số b > 0, phương trình đã cho vô nghiệm.

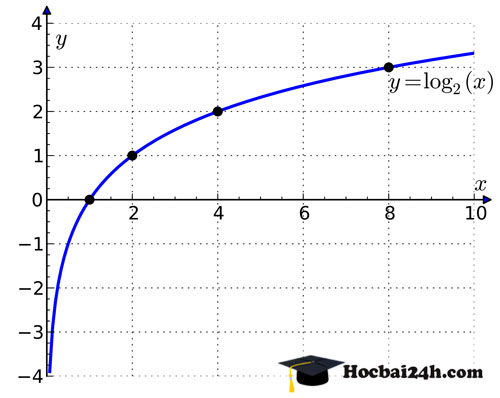
Tôi sẽ minh họa rõ hơn bằng đồ thị như sau:

Hoành độ giao điểm của đồ thị hai hàm số y = a^x  và y = b là nghiệm của phương a^x = b. Số nghiệm của phương trình đã cho là số giao điểm của hai đồ thị. Rõ ràng ta thấy, nếu b > 0 hai đồ thị luôn cắt nhau tại một điểm nên phương trình có nghiệm duy nhất. Còn nếu b ≤ 0  thì hai đồ thị không cắt nhau nên phương trình đã cho vô nghiệm.

Sau đây là một số cách giải phương trình mũ đơn giản

1.    Đưa về cùng cơ số

Dấu hiệu nhận biết : khi phương trình có cùng cơ số hoặc sau khi biến đổi ta có thể đưa phương trình về dạng cùng cơ số.

Ví dụ. Giải phương trình (5,5)^{9x – 1} = (\[\dfrac{{11}}{2}\])¹⁷

Giải. Ta đưa hai vế về cùng cơ số 5,5, ta được phương trình cơ bản đã biết cách giải 9x – 1 = 17.

1.    Đặt ẩn phụ

Dấu hiệu nhận biết : phương trình dễ dàng đưa về một ẩn duy nhất

Ví dụ. Giải phương trình 25^x - 4.5^x - 45 = 0.

Giải. Đặt t = 5^x, t > 0. Ta đưa phương trình về dạng căn bản đạ biết cách giải như sau t² – 4t – 45 = 0.

2.    Logarit hóa

Dấu hiệu nhận biết : khi không giải được bằng hai phương pháp trên và phương trình đã cho nếu lấy logarit hai bên đưa được về dạng đơn giản hơn ta sẽ áp dụng phương pháp này.