Nội dung

Gia sư biên hòa chia sẻ về hàm số lũy thừa

Bài trước tôi đã giới thiệu đến các bạn thế nào là lũy thừa của một số âm, lũy thừa với số mũ hữu tỉ, lũy thừa với số mũ vô tỉ, phương trình mũ căn bản và căn bậc n của một số. Hôm nay, tôi sẽ đưa các bạn đến bài học khá mới mẻ trong chương này đó là hàm số lũy thừa. Chúng ta sẽ cùng nhau nghiên cứu về khái niệm, đạo hàm của hàm lũy thừa và khảo sát hàm lũy thừa y = x^a nhé.

Khái niệm hàm số lũy thừa

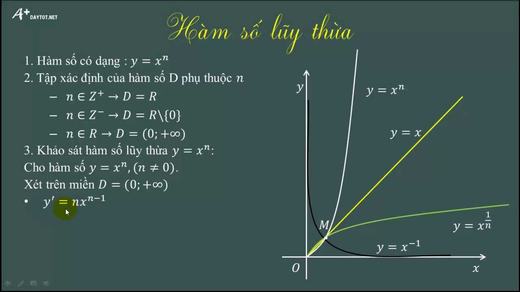
ham so luy thua

Ta đã biết một số hàm số như y = xⁿ với n thuộc tập hợp số tự nhiên, y = = 3x^-5, hay hàm số y = x^1/2 với mọi x > 0.

Bây giờ, gia sư biên hòa sẽ xét một cách tổng quát hàm số y = x^a với a là một số thực cho trước.

Hàm số y = x^a , với mọi số a thuộc tập số thực R, được gọi là hàm số lũy thừa.

Ví dụ

Hàm số y = 6x, y = 9x³, y = x^-3, y = x^2,5 là những hàm số hữu tỉ.

CHÚ Ý

Tập xác định của hàm số y = x^a tùy thuộc vào giá trị cùa a.

Với số a nguyên dương, tập xác định là R ;
Với số a nguyên âm hoặc bằng 0, tập xác định là R \ {0} ;
Với số a không nguyên, tập xác định là khoảng từ 0 đến dương vô cùng.

Đạo hàm của hàm lũy thừa

Lớp 11 ta đã biết đạo hàm của hàm số y = xⁿ với n ≥ 1 , n thuộc tập số tự nhiên N và hàm số y = là (x^x)’ = nx^n-1 với mọi x thuộc tập số thực R.

Tổng quát hơn, Trung tâm gia sư Biên Hòa đã chứng minh được rằng đạo hàm của hàm số lũy thừa y = x^a với a thuộc tập số thực R và với mọi x > 0 là

(x^a)’ = ax^a-1.

CHÚ Ý

Đối với hàm hợp, ta có công thức tính đạo hàm tổng quát như sau :

(u^a)’ = au^a-1u’.

bai tap ham so luy thua

Khảo sát hàm lũy thừa y = x^a

Ta có tập xác định của hàm số lũy thừa y = a^x luôn luôn chứa khoảng từ 0 đến dương vô cùng với mọi a thuộc tập số thực R. Trong một số trường hợp tổng quát, ta khảo sát hàm số y = x^a trên khoảng này ( gọi là tập khảo sát )

Ta sẽ chia 2 trường hợp để việc khảo sát trở nên dễ dàng hơn là a > 0 và a < 0.

a > 0 thì y’ = ax^a-1, hàm số luôn đồng biến, không có tiệm cận và đồ thị luôn đi qua điểm (1 ; 1).
a < 0 thì y’ = ax^a-1, hàm số luôn nghịch biến, tiệm cận ngang là trục Ox, tiệm cận đứng là trục Oy và đồ thị luôn đi qua điểm (1 ; 1).

Tôi là Trần Lai hiện đang là Co-Founder của Gia Sư Minh Trí. Trong blog của mình tôi chia sẻ các phương pháp học tập hiệu quả, các bài văn hay, thông tin về tác giả, tác phẩm để quý thầy cô, quý phụ huynh và các em học sinh tham khảo. Hi vọng sẽ giúp ích cho quý độc giả

Trần Lai

Các bài viết khác...